9. Rubik's Cube: index2singmaster 関数 ( SAGE )

小面のシングマスター記法

「群論の味わい」 David Joyner 著、川辺治之訳　の 91ページに次の文章がある。

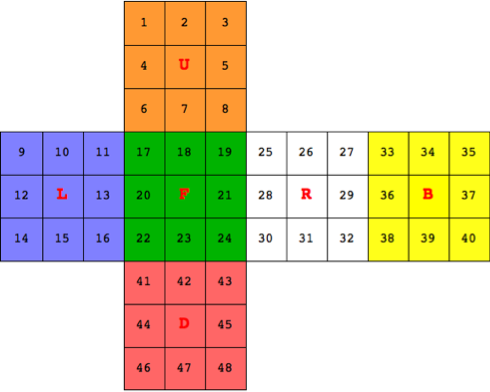
図4.3 のような番号付けが与えられたときに、SAGE を使って小面のシングマスター記法による表記を求めることができます。たとえば、41 と番号が付けられた小面は、シングマスター記法では dlf となります。

SAGE の例題を行ってみた。関数 index2singmaster を使用している。

次はsage -ipython notebookで実行した例です。設定方法は次のブログに書いてあります。

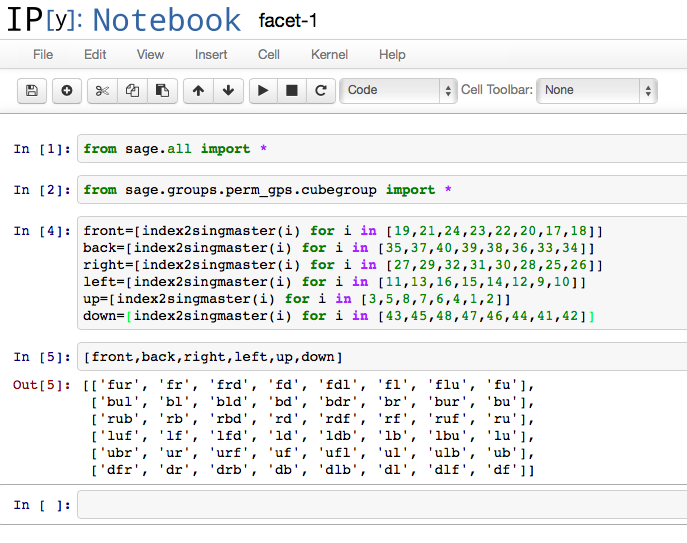
この表は p.90 に載っている表と違うところがある。この理由は小面を xyz と記述するときに、y と z の並べ方の規則に関係している。

Mathematica で index2singmaster 関数を作る

8. Rubik's Cube: 色配置リストから置換リストの変換　を基に関数を作った。

index2singmaster[n_] := 
 Module[{cornerSet, cornerAll, edgeSet, edgeAll, cubieAll, pos},
  (* corner cubie *)
  cornerSet = {{{1,9,35},{u,l,b}},{{3,33,27},{u,b,r}},
               {{6,17,11},{u,f,l}},{{8,25,19},{u,r,f}},
               {{14,46,40},{l,d,b}},{{16,22,41},{l,f,d}},
               {{24,30,43},{f,r,d}},{{32,38,48},{r,b,d}}};
  cornerAll = 
   Flatten[Function[x, NestList[Map[RotateRight,#]&,x,2]] /@ cornerSet,1];
  (*  edge cubie *)
  edgeSet = {{{2,34},{u,b}},{{4,10},{u,l}},{{5,26},{u,r}}, 
             {{7,18},{u,f}},{{12,37},{l,b}},{{13,20},{l,f}}, 
             {{21,28},{f,r}},{{29,36},{r,b}},{{15,44},{l,d}}, 
             {{23,42},{f,d}},{{31,45},{r,d}},{{39,47},{b,d}}};
  edgeAll = 
   Flatten[Function[x, NestList[Map[RotateRight, #] &, x, 1]] /@ edgeSet, 1];
  (*   *)
  cubieAll = Join[cornerAll, edgeAll];
  pos = Position[cubieAll[[All, 1, 1]], n][[1]][[1]];
  cubieAll[[pos, 2]]
  ]

関数の確認

front = {19, 21, 24, 23, 22, 20, 17, 18};
back = {35, 37, 40, 39, 38, 36, 33, 34};
right = {27, 29, 32, 31, 30, 28, 25, 26};
left = {11, 13, 16, 15, 14, 12, 9, 10};
up = {3, 5, 8, 7, 6, 4, 1, 2};
down = {43, 45, 48, 47, 46, 44, 41, 42};

frontSM= Table[ index2singmaster[i], {i, front}];
backSM = Table[ index2singmaster[i], {i, back}];
rightSM= Table[ index2singmaster[i], {i, right}];
leftSM = Table[ index2singmaster[i], {i, left}];
upSM   = Table[ index2singmaster[i], {i, up}];
downSM = Table[ index2singmaster[i], {i, down}];

{Join[{"front"}, frontSM], Join[{"back"}, backSM], Join[{"right"}, rightSM],
  Join[{"left"}, leftSM], Join[{"up"}, upSM], Join[{"down"}, downSM]}
⇒ {{"front", {f,u,r}, {f,r}, {f,r,d}, {f,d}, {f,d,l}, {f,l}, {f,l,u}, {f,u}},
{"back", {b,u,l}, {b,l}, {b,l,d}, {b,d}, {b,d,r}, {b,r}, {b,r,u}, {b,u}},
{"right", {r,u,b}, {r,b}, {r,b,d}, {r,d}, {r,d,f}, {r,f}, {r,f,u}, {r,u}},
{"left", {l,u,f}, {l,f}, {l,f,d}, {l,d}, {l,d,b}, {l,b}, {l,b,u}, {l,u}},
{"up", {u,b,r}, {u,r}, {u,r,f}, {u,f}, {u,f,l}, {u,l}, {u,l,b}, {u,b}},
{"down", {d,f,r}, {d,r}, {d,r,b}, {d,b}, {d,b,l}, {d,l}, {d,l,f}, {d,f}}}

list2string := Function[x, StringJoin[ToString[#] & /@ x]]
Grid[{Join[{"front"}, 
   MapThread[ ToString[#1] <> " " <> #2 &, {front, list2string /@ frontSM}]],
  Join[{"back"}, 
   MapThread[ ToString[#1] <> " " <> #2 &, {back, list2string /@ backSM}]],
  Join[{"right"}, 
   MapThread[ ToString[#1] <> " " <> #2 &, {right, list2string /@ rightSM}]],
  Join[{"left"}, 
   MapThread[ If[#1 < 10, " " <> ToString[#1] <> " " <> #2, 
      ToString[#1] <> " " <> #2] &, {left, list2string /@ leftSM}]],
  Join[{"up"}, 
   MapThread[ If[#1 < 10, " " <> ToString[#1] <> " " <> #2, 
      ToString[#1] <> " " <> #2] &, {up, list2string /@ upSM}]],
  Join[{"down"}, 
   MapThread[ ToString[#1] <> " " <> #2 &, {down, list2string /@ downSM}]]},
 Dividers -> {{True, True}, {True, False}}, Frame -> True, 
 ItemSize -> 4, Spacings -> {{1, 1}, 0.5}]