3. Rubik's Cube : RubikGroupの定義

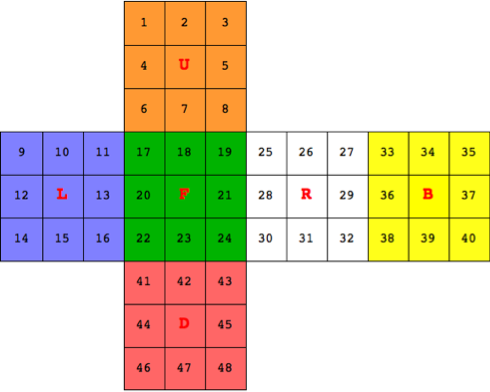
　参考文献 2, 3 と Mathematica チュートリアルにルービックキューブの定義が載っているが、面の命名や正面の番号付けが異なる。ここでは、図に示すような記述にする。ルービックキューブの定義について GAP, Sage とMathematicaを使ったコードを以下に示す。

GAP のコード

gap> u := (1,3,8,6)(2,5,7,4)(9,33,25,17)(10,34,26,18)(11,35,27,19);; 
gap> l := (9,11,16,14)(10,13,15,12)(1,17,41,40)(4,20,44,37)(6,22,46,35);; 
gap> f := (17,19,24,22)(18,21,23,20)(6,25,43,16)(7,28,42,13)(8,30,41,11);; 
gap> r := (25,27,32,30)(26,29,31,28)(3,38,43,19)(5,36,45,21)(8,33,48,24);; 
gap> b := (33,35,40,38)(34,37,39,36)(3,9,46,32)(2,12,47,29)(1,14,48,27);; 
gap> d := (41,43,48,46)(42,45,47,44)(14,22,30,38)(15,23,31,39)(16,24,32,40);;
gap> cube := Group(u,l,f,r,b,d);
< permutation group with 6 generators > 
gap> Size(cube);
43252003274489856000
gap> Collected(Factors(last));
[[2,27],[3,14],[5,3],[7,2],[11,1]]
gap> orbits := Orbits(cube,[1..48]);
[[1,3,17,14,8,38,9,41,19,48,22,6,30,33,43,11,46,40,24,27,25,35,16,32], 
[2,5,12,7,36,10,47,4,28,45,34,13,29,44,20,42,26,21,37,15,31,18,23,39]]
gap>

Sage のコード

sage: f = [(17,19,24,22),(18,21,23,20),(6,25,43,16),(7,28,42,13),(8,30,41,11)]
sage: b = [(33,35,40,38),(34,37,39,36),(3,9,46,32),(2,12,47,29),(1,14,48,27)]
sage: l = [(9,11,16,14),(10,13,15,12),(1,17,41,40),(4,20,44,37),(6,22,46,35)]
sage: r = [(25,27,32,30),(26,29,31,28),(3,38,43,19),(5,36,45,21),(8,33,48,24)]
sage: u = [(1,3,8,6),(2,5,7,4),(9,33,25,17),(10,34,26,18),(11,35,27,19)]
sage: d = [(41,43,48,46),(42,45,47,44),(14,22,30,38),(15,23,31,39),(16,24,32,40)]
sage: cube = PermutationGroup([f,b,l,r,u,d])
sage: cube.order()
43252003274489856000
sage :

Mathematica のコード

rotF = Cycles[{{17,19,24,22},{18,21,23,20},{6,25,43,16},{7,28,42,13},{8,30,41,11}}]; 
rotB = Cycles[{{33,35,40,38},{34,37,39,36},{3,9,46,32},{2,12,47,29},{1,14,48,27}}]; 
rotL = Cycles[{{9,11,16,14},{10,13,15,12},{1,17,41,40},{4,20,44,37},{6,22,46,35}}]; 
rotR = Cycles[{{25,27,32,30},{26,29,31,28},{3,38,43,19},{5,36,45,21},{8,33,48,24}}];
rotU = Cycles[{{1,3,8,6},{2,5,7,4},{9,33,25,17},{10,34,26,18},{11,35,27,19}}]; 
rotD = Cycles[{{41,43,48,46},{42,45,47,44},{14,22,30,38},{15,23,31,39},{16,24,32,40}}];
cube = PermutationGroup[{rotF,rotB,rotL,rotR,rotU,rotD}]; 
GroupOrder[cube] 
⇒ 43252003274489856000 
FactorInteger[GroupOrder[cube]] 
⇒ {{2,27},{3,14},{5,3},{7,2},{11,1}} 
orbits = GroupOrbits[cube,Range[48]] 
⇒ {{1,3,6,8,9,11,14,16,17,19,22,24,25,27,30,32,33,35,38,40,41,43,46,48}, 
{2,4,5,7,10,12,13,15,18,20,21,23,26,28,29,31,34,36,37,39,42,44,45,47}}

GAP, Sage とMathematica の対応を読み取る

巡回置換の記述の比較

GAP: u := (1,3,8,6)(2,5,7,4)(9,33,25,17)(10,34,26,18)(11,35,27,19);; 
Sage: u = [(1,3,8,6),(2,5,7,4),(9,33,25,17),(10,34,26,18),(11,35,27,19)] 
MMA: rotU = Cycles[{{1,3,8,6},{2,5,7,4},{9,33,25,17},{10,34,26,18},{11,35,27,19}}];