ブログを書いていて疑問に思ったことがある。キューブの配置リストでは数字(index)を使うことを前提にしている。しかし、実際のキューブには数字は書かれていない。色だけです。これまでの議論は数字の配置リストがあることが前提でした。色の配置リストから数字の配置リストを求めることはできるでしょうか?実はできるのです。
色を使ってキューブの面を指定する方法は、キューブの制作会社によって色が違うことがあり混乱を生じさせる。これを避ける方法として、位置に関連した名前 (Positional Names for Cube Faces) として、Singmaster 氏が Front(前面), Back(後面), Right,(右面) Left(左面), Up(上面), Down(下面) を導入した。これを シングマスター記法と呼ぶ。
シングマスター記法の Front(前面)の色を f とし、同様に、b, r, l, u, d とする。面の色を使った配置リスト ( q0 ) から数字の配置リスト ( p0 ) を求める関数を作ることにする。例として、q0 と p0 を次とする。
q0
⇒ {u,u,u,u,u,u,u,u,l,l,l,l,l,l,l,l,f,f,f,f,f,f,f,f,
r,r,r,r,r,r,r,r,b,b,b,b,b,b,b,b,d,d,d,d,d,d,d,d}
p0
⇒ { 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,
25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48}
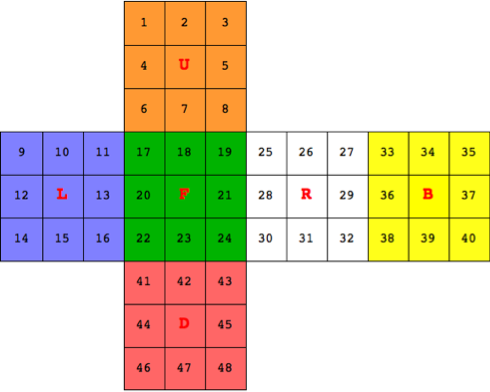
Corner cubie
完成された配置では、コーナーキューブ {1, 9, 35} は シングマスター記法の {u, l, b} に対応している。8個のコーナーキュービーについて記述したリストを cornerSet とする。
cornerSet = {{{1,9,35},{u,l,b}}, {{3,33,27},{u,b,r}},
{{6,17,11},{u,f,l}}, {{8,25,19},{u,r,f}},
{{14,46,40},{l,d,b}}, {{16,22,41},{l,f,d}},
{{24,30,43},{f,r,d}}, {{32,38,48},{r,b,d}}};コーナーの位置(cubicle) に入るべきコーナーキュービーの配置は、回転の自由度 3 を考慮すると24個になる。たとえば、コーナーキュービー {1, 9, 35} は、ひねると {35, 1, 9} になり、更にひねると {9, 35, 1} なる。もう一度ひねると元にもどる。8個のコーナーキューブについて行えば全てのコーナーキュービーの配置 cornerAll を作ることができる。
cornerAll = Flatten[Function[x, NestList[Map[RotateRight,#]&, x, 2]] /@ cornerSet, 1]
⇒ {{{1,9,35},{u,l,b}}, {{35,1,9},{b,u,l}}, {{9,35,1},{l,b,u}},
{{3,33,27},{u,b,r}}, {{27,3,33},{r,u,b}}, {{33,27,3},{b,r,u}},
{{6,17,11},{u,f,l}}, {{11,6,17},{l,u,f}}, {{17,11,6},{f,l,u}},
{{8,25,19},{u,r,f}}, {{19,8,25},{f,u,r}}, {{25,19,8},{r,f,u}},
{{14,46,40},{l,d,b}}, {{40,14,46},{b,l,d}}, {{46,40,14},{d,b,l}},
{{16,22,41},{l,f,d}}, {{41,16,22},{d,l,f}}, {{22,41,16},{f,d,l}},
{{24,30,43},{f,r,d}}, {{43,24,30},{d,f,r}}, {{30,43,24},{r,d,f}},
{{32,38,48},{r,b,d}}, {{48,32,38},{d,r,b}}, {{38,48,32},{b,d,r}}Edge cubie
完成された配置では、エッジキュービー {2, 34} は シングマスター記法で {u, lb} に対応している。12 個のエッジキュービーについて記述したリストは edgeSet です。
edgeSet = {{{2, 34}, {u, b}} , {{4, 10}, {u, l}}, {{5, 26}, {u, r}}, {{7, 18}, {u, f}},
{{12, 37}, {l, b}}, {{13, 20}, {l, f}}, {{21, 28}, {f, r }}, {{29, 36}, {r, b}},
{{15, 44}, {l, d}}, {{23, 42}, {f, d}}, {{31, 45}, {r, d}}, {{39, 47}, {b, d}}};エッジの位置に入るべきエッジュービーの配置は、入れ替えの自由度 2 を考慮すると24個になる。 たとえば、エッジキュービー {2, 34} は、入れ替えると {34, 2} になる。12 個のエッジキュービーについて行えば、全ての配置 edgeAll を作ることができる。
edgeAll = Flatten[Function[x, NestList[Map[RotateRight, #] &, x, 1]] /@ edgeSet, 1]
⇒ {{{2, 34}, {u, b}}, {{34, 2}, {b, u}}, {{4, 10}, {u, l}}, {{10, 4}, {l, u}},
{{5, 26}, {u, r}}, {{26, 5}, {r, u}}, {{7, 18}, {u, f}}, {{18, 7}, {f, u}},
{{12, 37}, {l, b}}, {{37, 12}, {b, l}}, {{13, 20}, {l, f}}, {{20, 13}, {f, l}},
{{15, 44}, {l, d}}, {{44, 15}, {d, l}}, {{21, 28}, {f, r}}, {{28, 21}, {r, f}},
{{23, 42}, {f, d}}, {{42, 23}, {d, f}}, {{29, 36}, {r, b}}, {{36, 29}, {b, r}},
{{31, 45}, {r, d}}, {{45, 31}, {d, r}}, {{39, 47}, {b, d}}, {{47, 39}, {d, b}}}
関数 singmaster2perm[q0_List]
色リスト q0 のうち cornerSet の1番目のコーナーの場所 {1, 9, 35} に入っているキュービーの色をシングマスター記法( u, l, f, r, b, d )で表示し、この色の組み合わせと同じものを cornerAll から探す出すことにより数字に変換する。次に2番面のコーナーの場所 {3, 33, 27} について同様に行う。この手続きを8 個のコーナーについて実行する。 更に、12個のエッジについて edgeSet と edgeAll を使って同様な操作を行う。 この手順を関数にしたものが 次の singmaster2perm である。
singmaster2perm[q0_List] := Module[{cornerSet, cornerAll, ttCorner, rulesCorner, edgeSet, edgeAll, ttEdge, rulesEdge},
(* corner *)
Clear[u, l, f, r, b, d];
cornerSet = {{{1, 9, 35}, {u, l, b}}, {{3, 33, 27}, {u, b, r}},
{{6, 17, 11}, {u, f, l}}, {{8, 25, 19}, {u, r, f}},
{{14, 46, 40}, {l, d, b}}, {{16, 22, 41}, {l, f, d}},
{{24, 30, 43}, {f, r, d}}, {{32, 38, 48}, {r, b, d}}};
cornerAll =
Flatten[Function[x, NestList[Map[RotateRight, #] &, x, 2]] /@ cornerSet, 1];
ttCorner = Flatten[
Table[
Table[
Function[x, If[q0[[x[[1]]]] === cornerAll[[i]][[2]],
Append[{x[[1]]}, cornerAll[[i]][[1]]] ]]@cornerSet[[j]],
{i, 1, 24}] // DeleteCases[#, Null] &,
{j, 1, Length[cornerSet]}],
1];
rulesCorner = Flatten[Function[x, MapThread[#1 -> #2 &, x]] /@ ttCorner, 1];
(* edge *)
edgeSet = {{{2, 34}, {u, b}} , {{4, 10}, {u, l}}, {{5, 26}, {u,
r}}, {{7, 18}, {u, f}},
{{12, 37}, {l, b}}, {{13, 20}, {l, f}}, {{15, 44}, {l, d}}, {{21,
28}, {f, r }}, {{23, 42}, {f, d}}, {{29, 36}, {r, b}}, {{31,
45}, {r, d}}, {{39, 47}, {b, d}}};
edgeAll =
Flatten[Function[x, NestList[Map[RotateRight, #] &, x, 1]] /@ edgeSet, 1];
ttEdge = Flatten[
Table[
Table[
Function[x, If[q0[[x[[1]]]] === edgeAll[[i]][[2]],
Append[{x[[1]]}, edgeAll[[i]][[1]]] ]]@edgeSet[[j]],
{i, 1, Length[edgeAll]}] // DeleteCases[#, Null] &,
{j, 1, Length[edgeSet]}],
1];
rulesEdge = Flatten[Function[x, MapThread[#1 -> #2 &, x]] /@ ttEdge, 1];
(* *)
ReplacePart[ReplacePart[q0, rulesCorner], rulesEdge]
]確認
q0 = {u, u, u, u, u, u, u, u, l, l, l, l, l, l, l, l,
f, f, f, f, f, f, f, f, r, r, r, r, r, r, r, r,
b, b, b, b, b, b, b, b, d, d, d, d, d, d, d, d};
singmaster2perm[q0]
⇒ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36,
37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48}
plotCube[p0]
右面で90°回転した例の場合。
qr = {u, u, f, u, f, u, u, f, l, l, l, l, l, l, l, l, f, f, d, f, d,
f, f, d, r, r, r, r, r, r, r, r, u, b, b, u, b, u, b, b, d, d, b, d, b, d, d, b};
pr = singmaster2perm[qr]
⇒ {1, 2, 19, 4, 21, 6, 7, 24, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
43, 20, 45, 22, 23, 48, 30, 28, 25, 31, 26, 32, 29, 27, 8, 34, 35, 5,
37, 3, 39, 40, 41, 42, 38, 44, 36, 46, 47, 33}
plotCube[pr]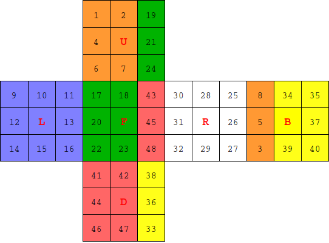
まとめ
- シングマスター(singmaster)記法について
- 8個のコーナーキュービーと12個のエッジキュービーを考慮に入れると色配置リストからインデックス配置リストに変換することができる。
- 関数 singmaster2perm[q0_List] を作った。