目次へ
"群論の味わい" David Joyner, 川辺 治之(訳) の 7章 7.4 に 「15パズルのグラフ理論」の説明が書いてある。特に次の文が目にとまった。
x0 を起点とする閉路の集合は (経路の合成について) 群になる。これを x_0 を起点とする \[CapitalGamma] のホモトピー群 といい、 \[CapitalGamma] (x0) と表記します。
The set of closed paths based x0 forms a group(under composition of paths) called the homotopy group of \[CapitalGamma] based at x0, denoted \[CapitalGamma] (x0).
具体的なホモトピー群 \[CapitalGamma] (x0) の求め方? を知りたいのだが載っていない。 Mathematica を使って 2x2 , 2x3 と 3x3 のグリッドグラフを表現し、未解決の課題の説明として載せることにする。
グリッドグラフ G2,2 の場合

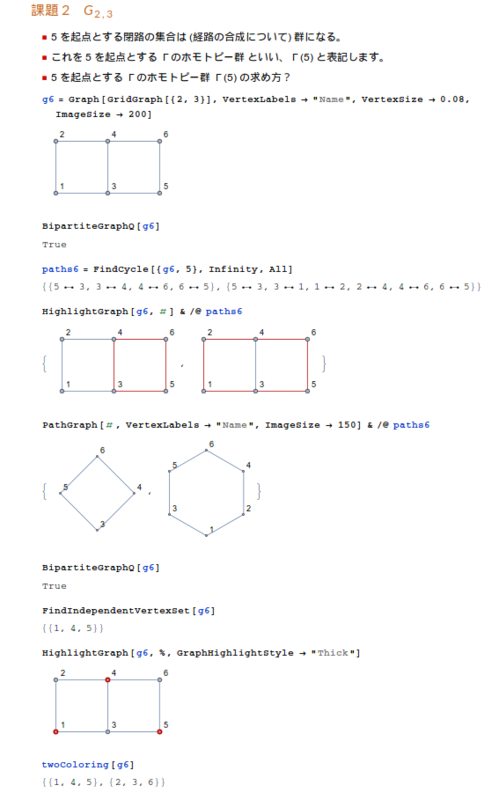
グリッドグラフ G2,3 の場合
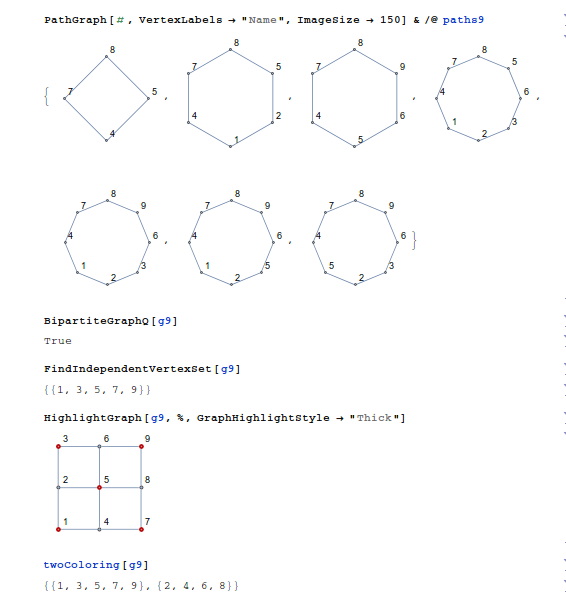
グリッドグラフ G3,3 の場合

まとめ
- Mathematica を使って "15パズル"をグラフで表現し分析することを目的にする。
- 置換群の場合、生成元から群を生成する関数 PermutationGroup があるが、
x0 を起点とする閉路の集合から (経路の合成について) 群 を作る方法がわからない。
これが解決したい課題である。
備忘録:
作業フォルダ: /workmath/15puzzle/Vojda-Graph/work-Graph/Agenda-Question/blog