6. Rubik's Cube: 回転について

回転の表現

「3. Rubik's Cube: RubikGroup の定義」を再度ここに載せる。

rotF = Cycles[{{17,19,24,22},{18,21,23,20},{6,25,43,16},{7,28,42,13},{8,30,41,11}}];
rotB = Cycles[{{33,35,40,38},{34,37,39,36},{3,9,46,32},{2,12,47,29},{1,14,48,27}}];
rotL = Cycles[{{9,11,16,14},{10,13,15,12},{1,17,41,40},{4,20,44,37},{6,22,46,35}}];
rotR = Cycles[{{25,27,32,30},{26,29,31,28},{3,38,43,19},{5,36,45,21},{8,33,48,24}}];
rotU = Cycles[{{1,3,8,6},{2,5,7,4},{9,33,25,17},{10,34,26,18},{11,35,27,19}}];
rotD = Cycles[{{41,43,48,46},{42,45,47,44},{14,22,30,38},{15,23,31,39},{16,24,32,40}}];
RubikGroup = PermutationGroup[{rotF, rotB, rotL, rotR, rotU, rotD}];

ここに現れた、rotF ,rotB, rotL, rotR ,rotU, rotD は回転に関する巡回置換である。次の関数で時計回りの回転を定義する。( 注: 関数 rotate を更新した。 3-Aug-2014 )

rotate[p_,rot_] := p[[#]]& /@ Permute[Range[48],rot]

rotR は右の面を時計回りに90°回転させる演算子になっている。

Needs["PlotRubiksCube`"]    (*  パッケージの読み込み  *)
p0 = Range[48];
p1 = rotate[ p0, rotR ];
PlotCube3D[ p1 ]

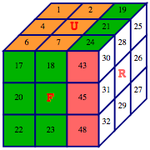
同様に、rotF は手前面( Front)、rotBは後面 (Back)、rotL は左面 (Left)、rotU は上面(Up)、rotD は底面(Down) の回転を表している。

連続して回転する場合には Fold 関数を使って記述できる。例とし右面の回転に続いて上面を回転する場合次になる。

p0 = Range[48];
p2 = Fold[ rotate, p0, {rotR, rotU} ];
PlotCube3D[ p2 ]

逆回転について

逆回転は関数 InversePermutation を使って表現できる。また、置換の積は PermutationProduct 関数がある。右面を時計回りに回転した後、反時計回りに回転すると元にもどることを次に示す。

PermutationProduct[rotR, InversePermutation[rotR]]
⇒ Cycles[{}]

右面、上面と回転した後、もとに戻す回転は次のように書ける。

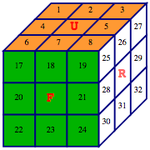
pRUUinvRinv = Fold[rotate, p0, {rotR, rotU, InversePermutation[rotU], InversePermutation[rotR]}];
pRUUinvRinv == Range[48]
⇒ True
PlotCube3D[ pRUUinvRinv ]