WXYZ-Wing-4222 の判別関数と探索関数: sudokuwiki.org

Sudokuwiki.org に WXYZ-Wing の解説が載っている。

図を見ていると分かったような気になるがプログラムを作るために WXYZ-Wing を判別する次のアルゴリズムを作った。この配置の特徴を示すため WXYZ-Wing-4222 と呼ぶことにする。

データ構造を{ {{W,X,Y, Z},{W,Z}, {X, Z}, {Y, Z} }, { {x, y}, {u, v}, {w, z},{ i, j } } } と表すことにする。 {{x, y}, {u, v}, {w, z}, { i, j }} はそれぞれのセルの番地とする。
条件1.
{ {W, X, Y, Z}, {W, Z}, {X, Z},{Y, Z} } は Naked Quads の 4/2/2/2 に属している。クリック here.
条件2.
{W, X, Y, Z} は幹 (stem) を意味する。{W,Z}, {X, Z} と {Y, Z} は枝 (branch) を表す。書き直すと { stem, branch1, branch2, branch3 } になる。
この配置では幹と枝の要素の数が {4, 2, 2, 2} なので WXYZ-Wing-4222 と呼ぶことにする。
条件3.
branch2 と branch3 はstem が入っている box 外にあり、 stem と横 (行) または縦 (列) に並んでいる。すなわち、w == x && z != y または w != x && z == y である。
1. branch2 と branch3 は同じ box 内でもよいし違うbox でもよい。
2. stem と branch2 の距離は、stem と branch3 の距離より小さいものとする。

条件4.
branch1 は stem が入っている box 内にあり、stem と{ branch2, branch3 }が並んだ行や列の外にある。
すなわち、IF x == w, u != x . IF y == z, v != y .
1. stem, branch2 と branch1 は直線上に並ばない。

Row:
stem {W, X, Y, Z} と { branch2 {X, Z} , branch3 {Y, Z} } が行に並んでいる場合：
1. stem {W, X, Y, Z} が属する box の中で、stem {W, X, Y, Z} と { branch2 {X, Z} , branch3 {Y, Z} } が入っている行にある Z を削除できる。
Column:
stem {W, X, Y, Z} と { branch2 {X, Z} , branch3 {Y, Z} } が列に並んでいる場合：
1. stem {W, X, Y, Z} が属する box の中で、stem {W, X, Y, Z} と { branch2 {X, Z} , branch3 {Y, Z} } が入っている列にある Z を削除できる。

次の WXYZ-Wing の例を使って次の Mathematica ノートブックで議論している。
次をクリックすると開きます。WXYZ-Wing-4222 notebook

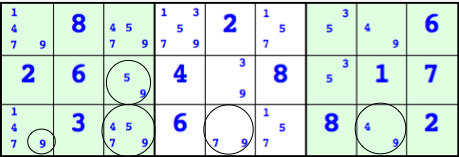
The Logic of Sudoku, p.59 の例

WXYZ-Wing-4222 のデータ構造を{ {{W,X,Y,Z}, {W, Z}, {X, Z}, {Y, Z}}, {{x, y}, {u, v}, {w, z}, {i, j} } } と表すことにする。 {{x, y}, {u, v}, {w, z}, {i, j} } はそれぞれのセルの番地とする。
WXYZ-Wing-4222 を判別する関数 wxyzWing4222Q[ data : {{{_, _, _,_}, {_, _}, {_, _}, {_, _}}, {{_, _}, {_, _}, {_, _}, {_, _}}} ] を作った。
WXYZ-Wing-4222 を見つける関数 findWXYZWing4222Delete2[ map_ } を作った。
見つけた WXYZWing-4222 のデータを使って削除できる番号と番地を求める関数 makeDeletelist2byXYZWing4222[ result_, map_] を作った。
これらの関数を基礎にして実用的なプログラムを作るのが課題です。