目次へ
前回で説明した複素関数をプロットするパッケージ ComplexMap.m を使う例を示す。
- 関数の定義に Function を使用している。
- 変数を変化させてグラフを表示できるようにグラフィックを動的に表示する Manipulate 関数を使っている。
- ノートブック と パッケージ ComplexMap.m が同じディレクトリにあるものとする。
複素関数  のプロット
のプロット
CartesianMap
mapfRow2[w_, a_] :=
GraphicsRow[{CartesianMap[ Identity,
{Re[w] - a, Re[w] + a}, {Im[w] - a, Im[w] + a},
PlotRange -> 5, Frame -> True,
FrameLabel -> Evaluate[Style[#, 13] & /@ {"x", "y"}]],
CartesianMap[ Function[z, Exp[z]],
{Re[w] - a, Re[w] + a}, {Im[w] - a,
Im[w] + a},
PlotRange -> 5,
FrameLabel -> Evaluate[Style[#, 13] & /@ {"u", "v"}],
Frame -> True]},
PlotLabel ->
Style["w = \!\(\*SuperscriptBox[\(\[ExponentialE]\), \(z\)]\)", 18,
Italic], ImageSize -> 400]
Manipulate[mapfRow2[x + I y, a],
{{x, 0}, -4, 4, Appearance -> "Labeled"},
{{y, 0}, -4, 4, Appearance -> "Labeled"}, {{a, 1.0}, 0.1, 2,
Appearance -> "Labeled"}]
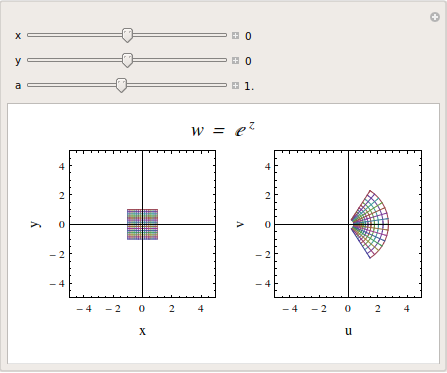
スライダーを動かしてみるには次をクリックする。 CartesianMap : w = exp(z)
PolarMap
mapfPolarRow2[w_, a_] :=
GraphicsRow[{PolarMap[ Function[z, z + w], {0, a}, {0, 2 Pi} ,
PlotRange -> 5, Frame -> True,
FrameLabel -> Evaluate[Style[#, 13] & /@ {"x", "y"}]],
PolarMap[ Function[z, Exp[z + w]], {0, a}, {0, 2 Pi},
PlotRange -> 5, Mesh -> False, Frame -> True,
FrameLabel -> Evaluate[Style[#, 13] & /@ {"u", "v"}]]},
PlotLabel ->
Style["w = \!\(\*SuperscriptBox[\(\[ExponentialE]\), \(z\)]\)", 18,
Italic],
ImageSize -> 400]
Manipulate[
mapfPolarRow2[x + I y, a], {{x, 0}, -4, 4,
Appearance -> "Labeled"}, {{y, 0}, -4, 4,
Appearance -> "Labeled"}, {{a, 1.5}, 0.1, 2,
Appearance -> "Labeled"}]
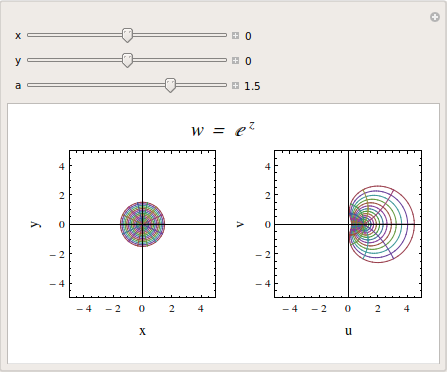
スライダーを動かしてみるには次をクリックする。 PolarMap : w = exp(z)
まとめ
- 複素関数の本に載っている図を参考にしてグラフを作ってみた。
- このノートブックをMathematica で実行し、スライダーを動かすことにより変数を変化させることができる。
- 変数を変化させた場合グラフはどのように変化するか、様子をみることができる。