目次へ
ボックス内で「隠れたシングル」を探す
「裸のシングル」 が見つからないゲームの行列は ini4 であった。ini4 については第9回を参照。
mapini4 = makeMap[ini4];
Show[Rasterize[plotMapGridsColoredByNakedSingle[ini4]], ImageSize -> 350]
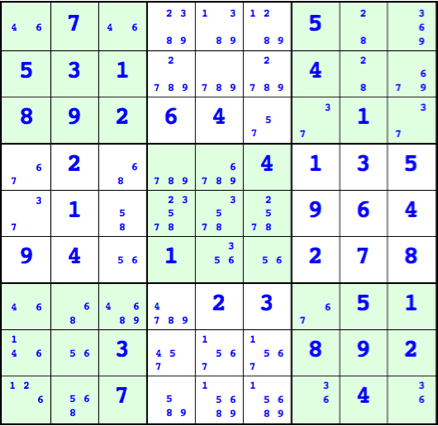
候補図の 4番目の ボックス ( 3x3 ) に注目する。3 は1個、5 は2個、6 は3個、7 は2個、8 は2個である。3は1個なので 「5行1列に 3を入れる」が答となる。
この作業をMathematica で表現する。4番目の box を取り出すと次になる。
box = mapini4[[4 ;; 6, 1 ;; 3]]
⇒ {{{6, 7}, {}, {6, 8}}, {{3, 7}, {}, {5, 8}}, {{}, {}, {5, 6}}}
ここで、ボックスの番号を入力したときにボックス( 3 x3 の行列) を取り出すための関数を作る。この関数を使うと、ボックスの番号 nbox を変数としてボックス( 3 x3 )の行列を取り出すことができる。1 番目のボックスと4 番目のボックスを取り出す場合について例を示す。
f[i_] := Which[1 <= i <= 3, 1 ;; 3, 4 <= i <= 6, 4 ;; 6, 7 <= i <= 9, 7 ;; 9];
g[j_] := Which[j == 1 || j == 4 || j == 7, 1 ;; 3,
j == 2 || j == 5 || j == 8, 4 ;; 6,
j == 3 || j == 6 || j == 9, 7 ;; 9];
nbox = 1; mapini4[[f[nbox], g[nbox]]]
⇒ {{{4, 6}, {}, {4, 6}}, {{}, {}, {}}, {{}, {}, {}}}
nbox = 4;
box = mapini4[[f[nbox], g[nbox]]]
⇒ {{{6, 7}, {}, {6, 8}}, {{3, 7}, {}, {5, 8}}, {{}, {}, {5, 6}}}
次に box 入っている数を取り出する。
Flatten[box, 1] (*内部の中括弧を外す。*)
⇒ {{6, 7}, {}, {6, 8}, {3, 7}, {}, {5, 8}, {}, {}, {5, 6}}
DeleteCases[Flatten[box, 1], {}]
⇒ {{6, 7}, {6, 8}, {3, 7}, {5, 8}, {5, 6}}
members = Flatten[DeleteCases[Flatten[box, 1], {}]] (*内部の中括弧を外す。*)
⇒ {6, 7, 6, 8, 3, 7, 5, 8, 5, 6}
個数を数える関数として Tally がある。次の結果が意味することは、リストの中で 5 を数えると1個、7 が 3個, 3 が 2個 を示している。次に1個の数を選び出す関数 Cases を使う。
Tally[members]
⇒ {{6, 3}, {7, 2}, {8, 2}, {3, 1}, {5, 2}}
Cases[Tally[members], {_, 1}]
⇒ {{3, 1}}
nums = Cases[Tally[members], {_, 1}][[All, 1]]
⇒ {3}
この数のbox の中での位置を求める。 3 の位置は2行1列の1番目を意味する。
Position[box, #] & /@ nums
⇒ {{{2, 1, 1}}}
Flatten[(Position[box, #] & /@ nums), 1]
⇒ {{2, 1, 1}}
pos = Flatten[(Position[box, #] & /@ nums), 1][[All, {1, 2}]]
⇒ {{2, 1}}
従って 3行3列の行列 box のなかでの位置は 2 行 1列である。これから 9行9列の行列 mapini4 の中の位置( 5行1 列)に変換する必要がある。次の便利な関数を使って実現する。
h[i_] :=
Which[i == 1, {0, 0}, i == 2, {0, 3}, i == 3, {0, 6},
i == 4, {3, 0}, i == 5, {3, 3}, i == 6, {3, 6},
i == 7, {6, 0}, i == 8, {6, 3}, i == 9, {6, 6}]
nbox = 4; h[nbox]
⇒ {3, 0}
pos99 = (# + h[nbox]) & /@ pos
⇒ {{5, 1}}
以上の手続きを関数にまとめる。
findHiddenSingleBox2[map_, nbox_] :=
Module[{f, g, h, maptmp, maptmpx, nums, pos, pos99},
(* begin{補助関数} *)
f[i_] := Which[1 <= i <= 3, 1 ;; 3, 4 <= i <= 6, 4 ;; 6, 7 <= i <= 9, 7 ;; 9];
g[j_] := Which[j == 1 || j == 4 || j == 7, 1 ;; 3,
j == 2 || j == 5 || j == 8, 4 ;; 6,
j == 3 || j == 6 || j == 9, 7 ;; 9];
h[i_] := Which[i == 1, {0, 0}, i == 2, {0, 3}, i == 3, {0, 6},
i == 4, {3, 0}, i == 5, {3, 3}, i == 6, {3, 6},
i == 7, {6, 0}, i == 8, {6, 3}, i == 9, {6, 6}];
(* end{補助関数} *)
maptmp = Table[{}, {9}, {9}];
maptmp = map;
(maptmpx = maptmp[[f[nbox], g[nbox]]];
nums = Cases[Tally[Flatten[maptmpx]], {_, 1}][[All, 1]];
pos = Flatten[(Position[maptmpx, #] & /@ nums), 1][[All, {1, 2}]];
pos99 = (# + h[nbox]) & /@ pos; (* Print[pos];Print[
pos99]; *)
{nums, pos99})
]
(* 全ての行について調べる関数は次になる。*)
findHiddenSingleBox[map_] := Module[{tmp},
tmp = DeleteCases[
Table[findHiddenSingleBox2[map, nbox], {nbox, 1, 9}], {{}, {}}];
If[tmp == {}, {{{}, {}}},
Flatten[Function[x, MapThread[{#1, #2} &, x]] /@ tmp, 1]]
]
findHiddenSingleBox[mapini4]
⇒ {{5, {3, 6}}, {3, {5, 1}}, {9, {7, 3}}, {2, {9, 1}}, {7, {7, 7}}}
プロットに関する関数は次になる。
findHiddenSingleBoxColor[map_] := Module[{tmp},
tmp = DeleteCases[
Table[findHiddenSingleBox2[map, nbox], {nbox, 1, 9}], {{}, {}}];
If[tmp == {}, {{{}, {}}},
Flatten[Function[x, MapThread[{{#1}, #2} &, x]] /@ tmp, 1]]
]
plotMapGridsColoredByHiddenSingleBox[ini_] :=
Module[{mapini, delList, grids},
mapini = makeMap[ini];
delList = findHiddenSingleBoxColor[mapini];
grids = makeGridsColored[makeGrids[mapini], delList, "Yellow"];
plotGridsColored[ini, grids]
]
Show[Rasterize[plotMapGridsColoredByHiddenSingleBox[ini4]], ImageSize -> 350]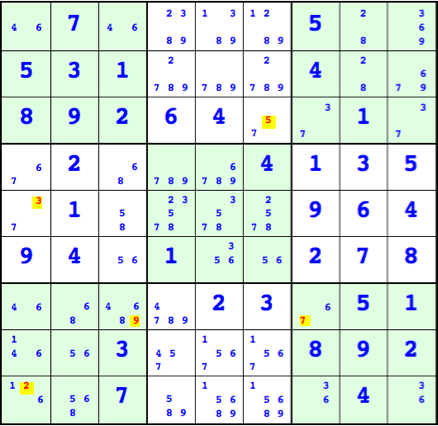
新しい行列を作る関数
makeMatrixByHiddenSingleBox[ini_] := Module[{mapini, singles},
mapini = makeMap[ini];
singles = findHiddenSingleBox[mapini];
rules = Map[Apply[Rule, Reverse[#]] &, singles];
Fold[ReplacePart[#1, #2] &, ini, rules]
]
ini5 = makeMatrixByHiddenSingleBox[ini4];
xylist = First[#] & /@ rules;
Show[Rasterize[plotGameSeq[ini5, xylist]], ImageSize -> 250]
新しく作った関数
findHiddenSingleBox2[map_, nrow_]findHiddenSingleBoxColor[map_]plotMapGridsColoredByHiddenSingleBox[ini_]makeMatrixByHiddenSingleBox[ini_]
次回は HiddenSingle をまとめたコード Code5 を示します。