目次へ
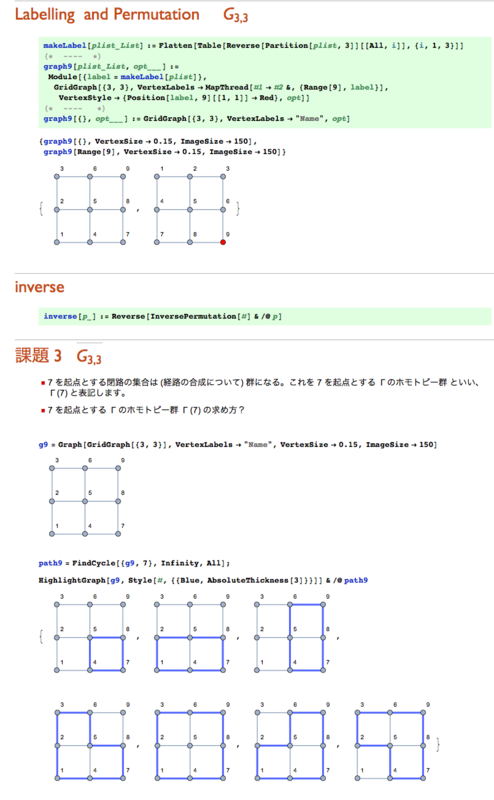
グリッドグラフ G3,3 で 8 puzzle を表現する
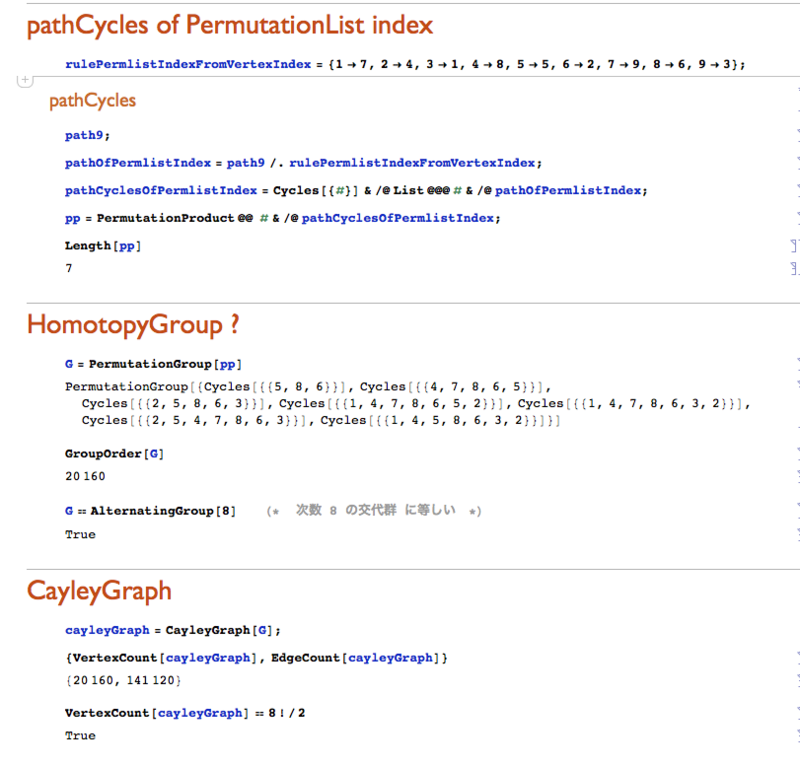
CayleyGraph を使って解法手順を求める
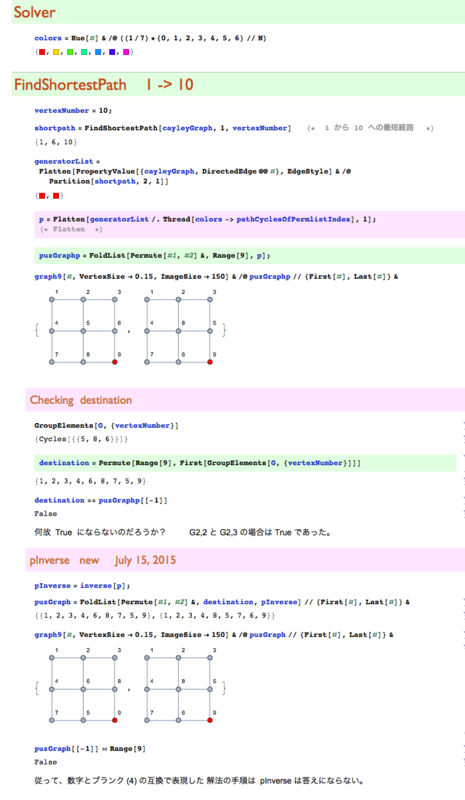
まとめ
- G3,3 の場合も G2,2 や G2,3 の場合と同じ手順で行ったが正解が得られない。
- 群の元の数が 8!/2 = 260160 と大きい場合の CalyGraph は正しいのだろうか?
- この CayleyGraph の正しさをどのようにすればチェックできるだろうか?
- ソルバーが行っていることは CayleyGraph をチェックしているように思えきた。
その後
Wolfram Communityに質問して次のことがわかった。
How to make colors of edges in CayleyGraph ?
- CayleyGraph は群の元の数が少ない場合に有効であるが、数百以上の場合複雑過ぎてバーテックスと辺の情報の利用については不具合が生じることがわかった。 G3,3 では使えない。
- 従って、CalyleGraph を使うのではなく、GroupElementoToWord 関数を使って解を求めたところ成功した。次のブログに載せることにする。
備忘録
~/Dropbox/workmath/15puzzle/Vojda-Graph/work-Graph/Agenda-Question/blog-G33/blog-G33-solver/blog-solver-G33-CayleyGraph-6-not.nb