目次へ
Vajda の本の 2ページに サイクルグラフ C4 の Puz-Graph が載っている。これをどのように作るかが疑問だった。
Steven Vajda, Mathematical Games and How to Play Them (Dover Books on Mathematics)
グリッドグラフ G2,2 の Puz-Graph が完成したので結果をここに載せることにする。説明は次のブログに回す。
グリッドグラフ G2,2
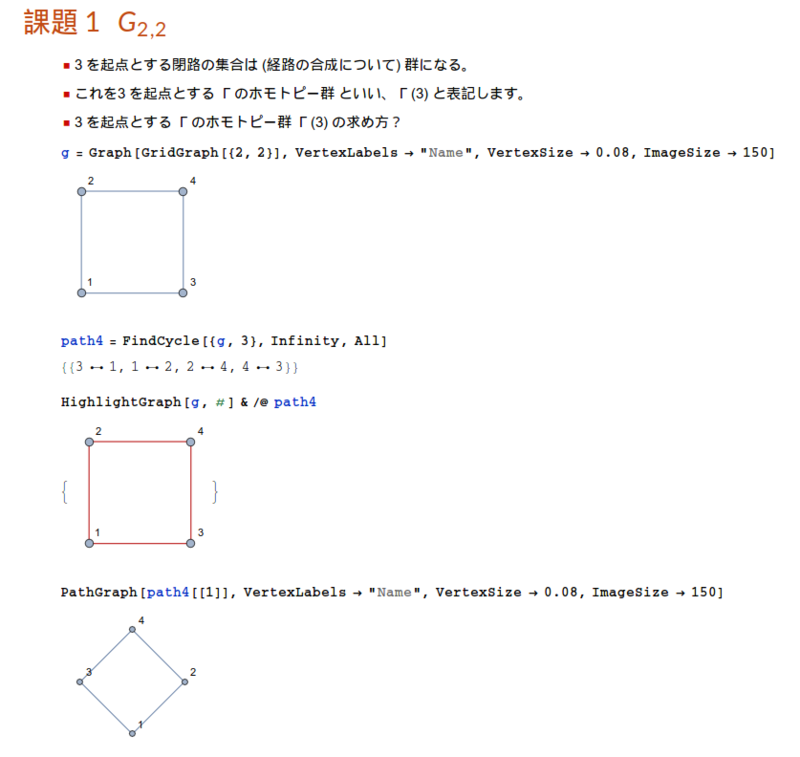
ラベリングと置換
Graph のバーテックスのインデックスは番地である。その番地にラベルをつけることによりラベルの配置を表現する。次の図の左は Graph のインデックスを表示し、右は パズルの番号付けを示している。

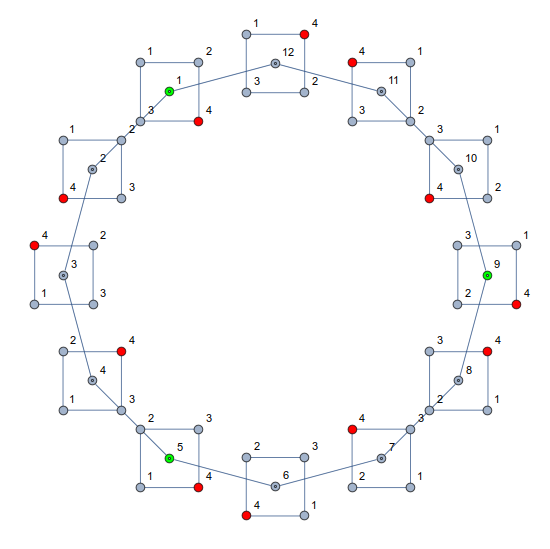
Puz-Graph
配置は12個あり、 4! /2 に等しい。右下が 4(赤)の配置は3個あり、第1,5 と 9 番のグラフです。この個数は 3! /2 に等しい。
まとめ
- 生成元から群を作る場合にケーリーグラフ( Cayley Graph ) の有用性が理解できた。
- これを手がかりに Puz-Graph を作ることができた。
備忘録:
作業フォルダ: /workmath/15puzzle/Vojda-Graph/work-Graph/Agenda-Question/blog-G22