12. Rubik's Cube: Mathematicaによる解法

目次へ

GAPを用いたRubik's Cube 解法表示ソフトについて田崎拓馬、藤本光史著　について Mathematicaを使って翻訳を試みた。

各面の表示を次のようにした。

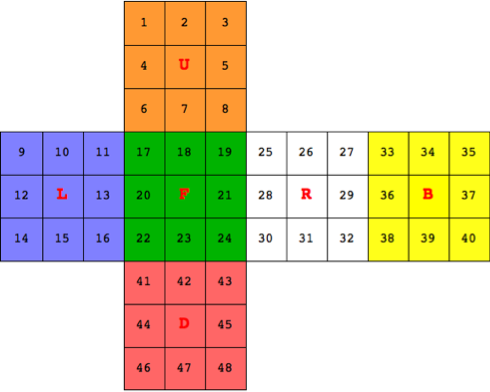
Mathematica のコード

(*  Mathematica code  *)
SetDirectory[NotebookDirectory[]];
<< PlotRubiksCube2.m
Names["PlotRubiksCube`*"]
⇒ {"PlotCube", "PlotCube3D"}
(*  *)
rotate[p_, rot_] := p[[#]] & /@ Permute[Range[48], rot]
(*  *)
rotF = Cycles[{{17,19,24,22},{18,21,23,20},{6,25,43,16},{7,28,42,13},{8,30,41,11}}];
rotB = Cycles[{{33,35,40,38},{34,37,39,36},{3,9,46,32},{2,12,47,29},{1,14,48,27}}];
rotL = Cycles[{{9,11,16,14},{10,13,15,12},{1,17,41,40},{4,20,44,37},{6,22,46,35}}];
rotR = Cycles[{{25,27,32,30},{26,29,31,28},{3,38,43,19},{5,36,45,21},{8,33,48,24}}];
rotU = Cycles[{{1,3,8,6},{2,5,7,4},{9,33,25,17},{10,34,26,18},{11,35,27,19}}];
rotD = Cycles[{{41,43,48,46},{42,45,47,44},{14,22,30,38},{15,23,31,39},{16,24,32,40}}];
cube = PermutationGroup[{rotF, rotB, rotR, rotL, rotU, rotD}];
GroupOrder[cube]
⇒ 43252003274489856000
FactorInteger[GroupOrder[cube]]
⇒ {{2, 27}, {3, 14}, {5, 3}, {7, 2}, {11, 1}}
(*  *)
rotSet = {rotF, rotB, rotR, rotL, rotU, rotD};
ruleRotate = {1 -> rotSet[[1]], 2 -> rotSet[[2]], 3 -> rotSet[[3]], 
   4 -> rotSet[[4]], 5 -> rotSet[[5]], 6 -> rotSet[[6]],
   -1 -> InversePermutation[rotSet[[1]]], -2 -> InversePermutation[rotSet[[2]]],
   -3 -> InversePermutation[rotSet[[3]]], -4 -> InversePermutation[rotSet[[4]]],
   -5 -> InversePermutation[rotSet[[5]]], -6 -> InversePermutation[rotSet[[6]]]};
rules = {"f"->1,"b"->2,"r"->3,"l"->4,"u"->5,"d"->6,"f^-1"->-1,
      "b^-1"->-2,"r^-1"->-3,"l^-1"->-4,"u^-1"->-5,"d^-1"->-6};
rules2 = {"f^2"->{1, 1},"r^2"->{3, 3},"f^-2"->{-1, -1},"r^-2"->{-3, -3}};

3.1 位数問題 -- 一連の操作を何回行うと元に戻るか

(* gap> Order(b*f^-1*l^-1*r^-1); *)
(* 12 *)
word = StringSplit["b*f^-1*l^-1*r^-1", "*"] /. rules
⇒ {2, -1, -4, -3}
perm = GroupElementFromWord[cube, word];
PermutationOrder[perm]
⇒ 12

3.2 メンバーシップ問題 -- 与えられた模様は実現可能か

(* gap> (8,19,25)(24,30,43) in cube; *)
(* true *)
GroupElementQ[cube, Cycles[{{8, 19, 25}, {24, 30, 43}}]]  
⇒ True

(* gap> (8,19,25)(24,43,30) in cube; *)
(* false  *)
GroupElementQ[cube, Cycles[{{8, 19, 25}, {24, 43, 30}}]] 
⇒ false

3.3 生成元の積で表す問題 -- Rubik's cube の完成手順を求める

(8,19,25)(24,30,43) で表される状態の配置

PlotCube3D[Permute[Range[48], Cycles[{{8,19,25},{24,30,43}}]]]

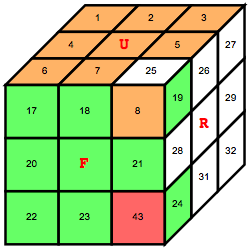
(* gap> GetWordOfElements:= function ( G, GenName, x )                          *)
(* >     local  gen, F, hom;                                                    *)
(* >     F := FreeGroup( GenName );                                             *)
(* >     gen := GeneratorsOfGroup( G );                                         *)
(* >     hom := GroupHomomorphismByImages( F, G, GeneratorsOfGroup( F ), gen ); *)
(* >     return PreImagesRepresentative( hom, x );                              *)
(* > end;                                                                       *)
(* function( G, GenName, x ) ... end                                               *)
(*                                                                                 *)
(* gap> p:= GetWordOfElements(cube,["f","b","r","l","u","d"],(8,19,25)(24,30,43)); *)
(* f*u*l*f*l^-1*f^-1*u^-1*f^-1*r^-1*f^-1*d^-1*f*d*r*f^2*r*f*r^-1*u*f^-1*u^-1*f*r*f^-1*r^-1*f*u^-1*r*u*r^-1*f *)

base = Complement[Range[48], Join[{8,19,25},{24,30,43}]];
p = GroupElementToWord[cube, Cycles[{{8,19,25}, {24,30,43}}], GroupActionBase -> base]
⇒ {1, -3, -2, 4, 2, 3, -2, -4, 2, -3, -2, 3, -1, -3, 2, 3}
Length[p]
⇒ 16
ppp = Fold[ rotate, Range[48], p /. ruleRotate ];
PlotCube3D[ppp]

得られた手順 p の逆元が完成手順を表す。

(* gap> p^-1; *)
(* f^-1*r*u^-1*r^-1*u*f^-1*r*f*r^-1*f^-1*u*f*u^-1*r*f^-1*r^-1*f^-2*r^-1*d^-1*f^-1*d*f*r*f*u*f*l*f^-1*l^-1*u^-1*f^-1 *)

pInverse = -1*Reverse[p]
⇒ {-3, -2, 3, 1, -3, 2, 3, -2, 4, 2, -3, -2, -4, 2, 3, -1}
ppinv = Fold[ rotate, ppp, pInverse /. ruleRotate ];
PlotCube3D[ppinv]

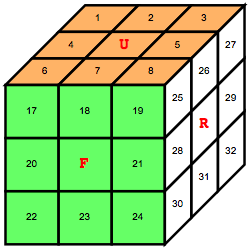
ルービックキューブを手で回して確認するために

手順 p

n2alpha = Reverse[#] & /@ rules
⇒ {1->"f",2->"b",3 ->"r",4->"l",5->"u",6->"d",-1->"f^-1",-2->"b^-1",-3->"r^-1",-4->"l^-1",-5 ->"u^-1",-6->"d^-1"}
p
⇒ {1, -3, -2, 4, 2, 3, -2, -4, 2, -3, -2, 3, -1, -3, 2, 3}
p /. n2alpha
⇒ {"f","r^-1","b^-1","l","b","r","b^-1","l^-1","b","r^-1","b^-1","r","f^-1","r^-1","b","r"}

手順 p^-1

pInverse
⇒ {-3, -2, 3, 1, -3, 2, 3, -2, 4, 2, -3, -2, -4, 2, 3, -1}
pInverse /. n2alpha
⇒ {"r^-1","b^-1","r","f","r^-1","b","r","b^-1","l","b","r^-1","b^-1","l^-1","b","r","f^-1"}