Sudoku(数独) を Mathematicaで解く(3) - makeMap

Mathematica sudoku

目次へ

3. 候補の求め方

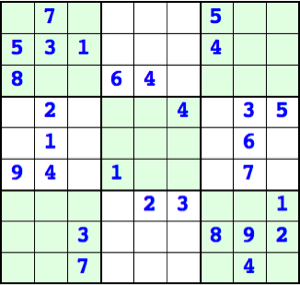
はじめに、1 行1列に入れるべき数の候補を検討する。Sudoku のルールによれば、１行に7と5 があるので 1 から9 の候補の数から 5, 7 が除かれる。１列に 5,8,9 があるので除かれる。1 行1列が属する 3x3 のブロックに 1,3,5,7,8 があるので候補から除かれる。従って、候補は 2,4,6 となる。これを Mathematica で表現する。

1 行目について

行列 ini から１行を取り出し、そこに含まれる数を選び出す。出力を ⇒ を使って表すことにします。

ini[[1]]
⇒ {Null, 7, Null, Null, Null, Null, 5, Null, Null}

Null を除くには関数 DeleteCases を使う

row = DeleteCases[ini[[1]], Null]
⇒ {7, 5}
１列について

行列 ini から１列を取り出し含まれる数を選び出す。

ini[[All, 1]]
⇒ {Null, 5, 8, Null, Null, 9, Null, Null, Null}

col = DeleteCases[ini[[All, 1]], Null]
⇒ {5, 8, 9}
3x3 のブロックについて

1行1列が属している 3x3 のブロックについて検討する。3x3 のブロックは次のようにして抜き取ることができる。

ini[[1;;3,1;;3]]
⇒ {{Null, 7, Null}, {5, 3, 1}, {8, Null, Null}}

波括弧が2重なっているので、内側の波括弧をFlatten を使って削除する。

Flatten[ini[[1;;3,1;;3]]]
⇒ {Null, 7, Null, 5, 3, 1, 8, Null, Null}

box = DeleteCases[Flatten[ini[[1;;3,1;;3]]], Null]
⇒ {7, 5, 3, 1, 8}
まとめると

row,colとboxの和集合を作る。

Union[row, col, box]
⇒ {1, 3, 5, 7, 8, 9}

候補の数の集合 {1,2,3,4,5,6,7,8,9} からこれを除いた数の集合が候補になる。

集合の引き算の関数は Complement であるから次のように書くことができる。

Complement[{1,2,3,4,5,6,7,8,9}, Union[row, col, box]]
⇒ {2, 4, 6}

ここで、1 から9の数からなるリストは、関数 Range[9] で作ることができるので、整理して書くと次になる。

Complement[Range[9], Union[row, col, box]]
⇒ {2, 4, 6}
追加説明

1 行2列には数が入っている。入れるべき数の候補は無いので、 { } で表現する。

一般化

以上を一般化して、i 行 j 列の場合を検討する。i 行を取り出すには ini[[i]] を使い、j 列を取り出すにはini[[All,j]] で取り出すことができる。ここで問題なのは、i 行 j 列が属する 3x3 ブロックの決定方法である。次の関数が解決してくれる。

f[i_]:=Which[1<=i<=3,1;;3, 4<=i<=6,4;;6, 7<=i<=9,7;;9]
f[1]
⇒ 1;;3

1 行1 列を含むブロックは ini[[1;;3,1;;3]]である。従って ini[[f[1],f[1]]]と書ける。

1 行4 列を含むブロックは ini[[1;;3,4;;6]]である。従って ini[[f[1],f[4]]]と書ける。

{f[1],f[4]}
⇒ {1;;3,4;;6}

関数の定義

i行j列の候補のリストをつくる関数 candidates は次になる。全ての要素について調べれば、候補のリストをつくる関数 makeMap になる。

candidates[ini_?MatrixQ,{i_,j_}]:=Module[{f},
  f[k_]:=Which[1<=k<=3, 1;;3,4<=k<=6,4;;6,7<=k<=9,7;;9];
  If[ini[[i,j]]=!=Null,{},
    Complement[Range[9],
    Union[ini[[i]],ini[[All,j]],Flatten[ini[[f[i],f[j]]]]]]
  ]
  ]
makeMap[ini_?MatrixQ]:=Table[candidates[ini,{i,j}],{i,1,9},{j,1,9}]

使い方

candidates[ini, {1, 1}]
⇒ {2, 4, 6}

mapini= makeMap[ini]
⇒ {{{2,4,6},{},{2,4,6,9},{2,3,8,9},{1,3,8,9},{1,2,8,9},{},{1,2,8},{3,6,8,9}},
  {{},{},{},{2,7,8,9},{7,8,9},{2,7,8,9},{},{2,8},{6,7,8,9}},
  {{},{9},{2,9},{},{},{1,2,5,7,9},{1,2,3,7,9},{1,2},{3,7,9}},
  {{6,7},{},{6,8},{7,8,9},{6,7,8,9},{},{1,9},{},{}},
  {{3,7},{},{5,8},{2,3,5,7,8,9},{3,5,7,8,9},{2,5,7,8,9},{2,9},{},{4,8,9}},
  {{},{},{5,6,8},{},{3,5,6,8},{2,5,6,8},{2},{},{8}},
  {{4,6},{5,6,8,9},{4,5,6,8,9},{4,5,7,8,9},{},{},{6,7},{5},{}},
  {{1,4,6},{5,6},{},{4,5,7},{1,5,6,7},{1,5,6,7},{},{},{}},
  {{1,2,6},{5,6,8,9},{},{5,8,9},{1,5,6,8,9},{1,5,6,8,9},{3,6},{},{3,6}}};

mapini//MatrixForm

f:id:MMAys:20181020221247p:plain

mapini=makeMap[ini];
Show[Rasterize[plotMapGrid[ini, mapini]], ImageSize -> 400]

関数 plotMapGrid は (2) で導入したものです。ただし、plotMapGrid ではこの図のように候補に色がつきません。色付けは後に説明します。

続く

次は、「候補図から解を見つける」を説明します。

目次へ