Sudoku(数独) を Mathematicaで解く(1) - 表現と表示

目次へ

「 Mathematica で「数独」を解くことができるか」の質問をうけ「できる」と答えたので無垢になってプログラム作りを始めたのがきっかけです。現在のプログラムは中級の問題を解くことができるところまで成長しました。

1. Mathematica による Sudoku(数独) の表現と表示

Sudoku(数独) を Mathematica で解くプログラムを作ることは、Mathematicaプログラミングの練習になります。ゲームを解くことは、Sudoku をリストで表現し、ゲームのルールに従った解を求める関数を作ることに相当します。

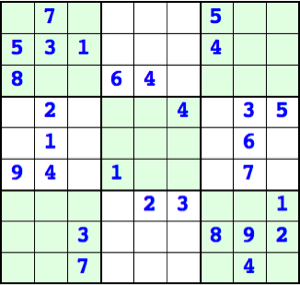
次の Sudoku(数独) の問題は、日経新聞10月19日(土) (2013)の付録に「ナンバープレース」として載っていたものです。Mathematica にデータを入力し描いたものです。

データは9行9列の行列( ini ) として表現します。

ini=Module[{b},{
   {b,7,b,b,b,b,5,b,b}, {5,3,1,b,b,b,4,b,b}, {8,b,b,6,4,b,b,b,b},
   {b,2,b,b,b,4,b,3,5}, {b,1,b,b,b,b,b,6,b}, {9,4,b,1,b,b,b,7,b},
   {b,b,b,b,2,3,b,b,1}, {b,b,3,b,b,b,8,9,2}, {b,b,7,b,b,b,b,4,b}
   }/.b->Null];

次に示す関数 plotGameを使って描くことができます。

plotGame[ini_?MatrixQ]:=Grid[ini,
   ItemStyle->{Directive[Blue,25,Bold],None},
   ItemSize->{2.5,2.5},Dividers ->
   {{{Thickness[2],True,True}},{{Thickness[2],True,True}}},
   Background -> {Automatic,Automatic,
   Flatten[Table[{i, j} -> If[EvenQ[Plus @@ Floor[{i - 1, j - 1}/3]],
   LightGreen, White], {i, 9}, {j, 9}]]},Spacings->{0,0.45}]